제조업 사례 (난이도 상)

제조업의 데이터분석은 금융업이나 소매업보다 조금 더 복잡합니다. 이 제조업 사례의 문제를 풀기 위해서는 두 가지 지식이 필요한데요. 하나는 최소자승법(Least Square Method)이고 다른 하나는 선형계획법(Linear Programming) 입니다. 철강업체 A 에서 환경관리를 담당하고 있는 여과장은 용해 후에 최종적으로 납품되는 Alloy(금속합금) 의 성분에 독성이 강한 X 물질이 다량 함유 되어 있다는 것을 알았습니다. 이 독성물질 X 는 함유율이 임계점 0.05% 이상되었을 때 독성이 강하게 나타납니다. 따라서, 최종 합금 Alloy 에 독성 물질이 0.05% 이하가 되도록 관리를 하고 싶습니다. Alloy 는 10 개의 공급 업체에서 금속 Scrap (스크랩) 를 납품받은 후, 몇 개의 업체 Scrap 을 선별 후, 용해해서 만듭니다. 첫 번째 문제는 각 업체에서 공급하는 Scrap 에 함유되어 있는 X 물질의 함유율을 정확히 모르고, 두 번째 문제는 X 물질의 함유율이 낮을 수 록 Scrap 단가가 비싸다는 것입니다. X 물질 함유율이 낮은 Scrap 만을 골라서 용해를 하면 독성 물질 X 함유율을 0.05% 이하로 관리할 수 있으나, 비용 증가의 문제가 생깁니다. 결국 풀고자하는 문제는 최소한의 비용으로 독성물질의 함유율이 0.05% 이하가 되도록 Alloy 합금을 만드는 것입니다.

여과장은 아래와 같이 배치( Batch) 데이터베이스를 만들었습니다. 아래 테이블은 샘플 배치 3 개를 보여주고 있습니다. 예를 들어 첫 번째 배치 B123 에는 3 개 업체의 Scrap 이 각 13톤, 5톤, 12톤이 투입되었습니다. 최종적으로 30 톤의 Alloy 가 만들어졌는데요. 독성물질 X 의 함유량을 측정해 보니 0.07% 가 들어있었고, 이 배치는 0.05% 를 넘어갔으므로 불합격입니다. 만약 여과장이 각 업체 Scrap 의 X 함유율 P1 ~ P10 을 알고 있다면, 최소비용으로 Alloy 를 만드는 방법을 선형계획법을 풀 수 가 있습니다. 먼저 선형 계획법으로 문제를 풀어보겠습니다.

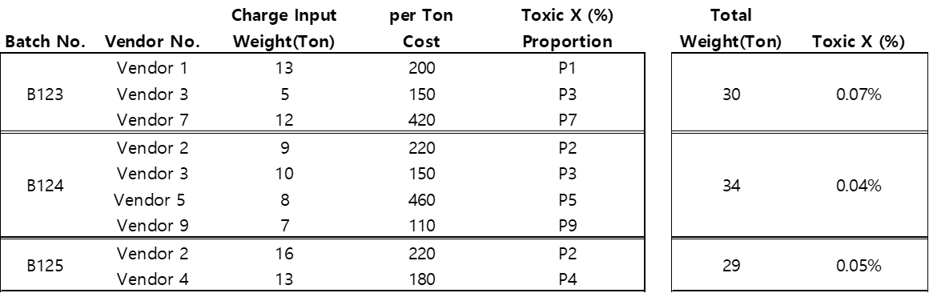
위 문제를 선형 계획법으로 도식화하면 아래와 같습니다. 배치의 총 비용을 목적함수으로 하고, 목적함수를 최소화하는 투입량 Wi 을 찾습니다. 단, 투입 후 물질 X 의 함유량이 0.05% 이하여야 한다는 제약이 있습니다. 아래에서 각 \( W,\ C,\ P \) 는 다음을 의미합니다. \( W \): Weight, \( C \): Cost, \( P \): Proportion

Minimize \( \sum\ \) \( [ W_i \) * \( C_i \ ] \) (비용 목적함수) for \( vendor = i \)

(제약식)

\( [ W_i \)* \( P_i \ ] \) \(\ <= \) \(∑ \ W_i \ * \ 0.05\% \) (물질 X 의 함유량 제약)
\( \sum\ W_i \) = (필요한 총 톤 수 제약)

이제 여과장은 각 업체의 물질 X 함유량 P 만 알면 위 선형계획법을 활용하여 최소비용으로 Alloy 를 생산하는 업체별 Scrap 투입량 W 를 알아낼 수 있습니다. 파이썬에서 선형계획법(Linear Programming) 은 PuLp 라이브러리에서 구현할 수 있습니다..

문제는 어떻게 함유량 P1 ~ P10 를 알아내는냐입니다. 사실 이 문제를 푸는 방법은 여러가지가 있습니다. 여과장은 최소자승법으로 문제를 풀었는데요. 어떻게 풀었는지 함 보겠습니다. 만약 우리가 P1 ~ P10 을 알고 있다면 각 배치별 물질 X 의 총량은 아래와 같이 추정할 수 있을 것입니다. 그렇다면 추정치 함유량과 실제 함유량의 차이가 최소가 되는 P1 ~ P10 을 찾는 것입니다.