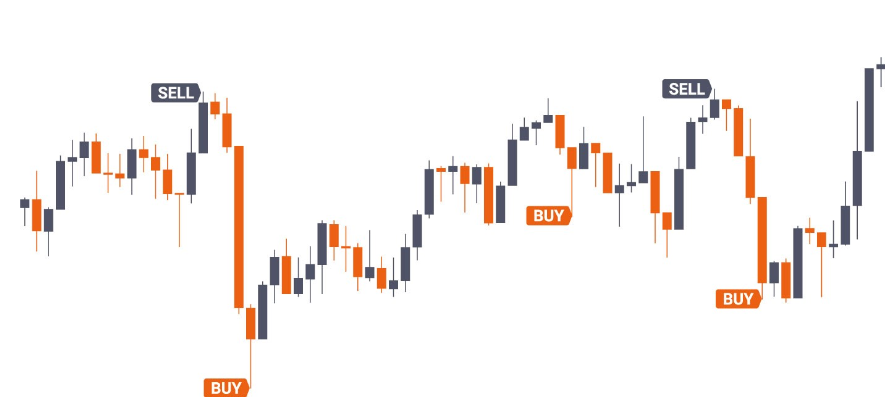
위 꼬리가 긴 양봉이 자주 발생한다.
import FinanceDataReader as fdr
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
pd.options.display.float_format = '{:,.3f}'.format
위 꼬리가 긴 양봉이 자주 발생한다.#
위 꼬리는 종가보다 고가가 더 높이 위치해 있는 양봉입니다. 따라서 고가를 종가로 나눈 값이 1 보다 상당히 크면 위꼬리 양봉이라고 할 수 있습니다. 양봉의 조건은 종가가 시가보다 큰 것입니다. 이 것을 데이터로 표현합니다.
mdl_data = pd.read_pickle('mdl_data.pkl')
mdl_data.head().style.set_table_attributes('style="font-size: 12px"')
| open | high | low | close | volume | change | code | name | kosdaq_return | return | win_market | close_r1 | close_r2 | close_r3 | close_r4 | close_r5 | max_close | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2021-01-05 | 2270 | 2285 | 2200 | 2250 | 410263 | -0.004425 | 060310 | 3S | 1.008326 | 0.995575 | 0 | 1.017778 | 1.017778 | 0.997778 | 0.966667 | 0.971111 | 1.017778 |
| 2021-01-06 | 2225 | 2310 | 2215 | 2290 | 570349 | 0.017778 | 060310 | 3S | 0.995567 | 1.017778 | 1 | 1.000000 | 0.980349 | 0.949782 | 0.954148 | 0.949782 | 1.000000 |
| 2021-01-07 | 2290 | 2340 | 2240 | 2290 | 519777 | 0.000000 | 060310 | 3S | 1.007612 | 1.000000 | 0 | 0.980349 | 0.949782 | 0.954148 | 0.949782 | 0.958515 | 0.980349 |
| 2021-01-08 | 2300 | 2315 | 2225 | 2245 | 462568 | -0.019651 | 060310 | 3S | 0.998918 | 0.980349 | 0 | 0.968820 | 0.973274 | 0.968820 | 0.977728 | 0.973274 | 0.977728 |
| 2021-01-11 | 2230 | 2275 | 2130 | 2175 | 409057 | -0.031180 | 060310 | 3S | 0.988702 | 0.968820 | 0 | 1.004598 | 1.000000 | 1.009195 | 1.004598 | 1.002299 | 1.009195 |
kosdaq_list = pd.read_pickle('kosdaq_list.pkl')
data_h3 = pd.DataFrame()
for code in kosdaq_list['code']:
data = mdl_data[mdl_data['code']==code].sort_index().copy()
data['positive_candle'] = (data['close'] > data['open']).astype(int) # 양봉
data['high/close'] = (data['positive_candle']==1)*(data['high']/data['close'] > 1.1).astype(int) # 양봉이면서 고가가 종가보다 높게 위치 10% 이상 높은 경우
data['num_high/close'] = data['high/close'].rolling(20).sum()
data['max_close'] = data[['close_r1','close_r2','close_r3','close_r4','close_r5']].max(axis=1) # 5 영업일 종가 수익율 중 최고 값
data.dropna(subset=['num_high/close','close_r1','close_r2','close_r3','close_r4','close_r5'], inplace=True) # missing 이 있는 행은 제거
data_h3 = pd.concat([data, data_h3], axis=0)
data_h3.to_pickle('data_h3.pkl')
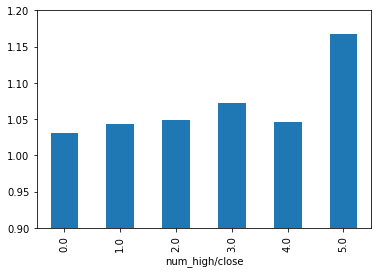
윗 꼬리가 긴 양봉이 많이 발생할 수 록 수익율에 좋은 영향을 주는 것으로 분석이 되었습니다.
data_h3 = pd.read_pickle('data_h3.pkl')
print(data_h3.groupby('num_high/close')['max_close'].agg(['count','mean']))
data_h3.groupby('num_high/close')['max_close'].mean().plot(kind='bar', ylim=(0.9,1.2)) # 막대그래프로 표현
count mean
num_high/close
0.000 355754 1.031
1.000 37734 1.043
2.000 5113 1.050
3.000 824 1.072
4.000 159 1.047
5.000 10 1.168
<AxesSubplot:xlabel='num_high/close'>
윗 꼬리가 긴 양봉도 궁금하지만, 장대양봉은 어떨지도 궁금합니다. 이렇게 가설을 검증하는 과정에서 새로운 가설을 테스트하기도 합니다. 장대양봉이 과거 60일 동안 몇 번 발생했는지 카운트해보고, 장대양봉의 갯 수와 수익율 사이에 상관성이 있는 지 함 보겠습니다.
kosdaq_list = pd.read_pickle('kosdaq_list.pkl')
data_h3 = pd.DataFrame()
for code in kosdaq_list['code']:
data = mdl_data[mdl_data['code']==code].sort_index().copy()
data['positive_candle'] = (data['close'] > data['open']).astype(int) # 양봉
data['long_candle'] = (data['positive_candle']==1)*(data['high']==data['close'])*\
(data['low']==data['open'])*(data['close']/data['open'] > 1.2).astype(int) # 장대 양봉을 데이터로 표현
data['num_long'] = data['long_candle'].rolling(60).sum() # 지난 20 일 동안 장대양봉의 갯 수
data['max_close'] = data[['close_r1','close_r2','close_r3','close_r4','close_r5']].max(axis=1) # 5 영업일 종가 수익율 중 최고 값
data.dropna(subset=['num_long','close_r1','close_r2','close_r3','close_r4','close_r5'], inplace=True) # missing 이 있는 행은 제거
data_h3 = pd.concat([data, data_h3], axis=0)
data_h3.to_pickle('data_h3.pkl')
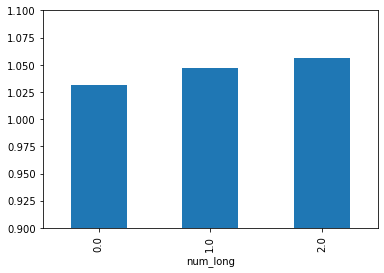
과거 60일 동안 장대양봉이 2 번 발생한 경우 좋은 수익율을 보여주고 있습니다.
data_h3 = pd.read_pickle('data_h3.pkl')
print(data_h3.groupby('num_long')['max_close'].agg(['count','mean']))
data_h3.groupby('num_long')['max_close'].mean().plot(kind='bar', ylim=(0.9,1.1))
count mean
num_long
0.000 337432 1.031
1.000 5394 1.047
2.000 88 1.056
<AxesSubplot:xlabel='num_long'>